Cercle

Déformation d'un cercle sous Cabri 3D

Déformation d'un triangle :

Observez la déformation d'un triangle en variant sa forme et la vitesse de déplacement.

Triangle

Déformation d'un triangle sous Cabri 3D

Déformation d'un polygone :

Idem pour un polygone.

Polygone inscrit
Polygone libre
Déformation d'un carré sous Cabri 3D

Déformation d'une ellipse :
Idem pour un conique (ellipse)

Cas d'une ellipse

Déformation d'une ellipse sous Cabri 3D

Déformation d'une droite :
Idem pour une droite

Cas d'une droite

Déformation d'une ligne droite sous Cabri 3D

Définition
Cône isodéviant

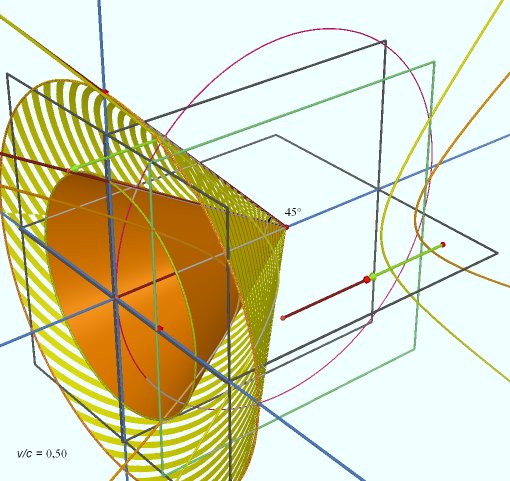
En 3D, le cône isodéviant définit l'angle solide pour lequel les rayons émis ont la même déviation pour une vitesse donnée.

L'équation du cône est :

z²+y²-tan(r).x²=0

si l'axe de déplacement est orienté sur l'axe des x.

L'équation du cône de visée est donc :

z²+y²-tan(r-t).x²=0

t étant l'angle de déviation relativiste.

Exemples graphiques de cônes isodéviants vu à différents v/c et angle par rapport à la direction de déplacement:

• v/c=0.1 avec un angle de 45°
• v/c=0.5 avec un angle de 45°
• v/c=0.8 avec un angle de 45°
• v/c=0.5 avec un angle de 22°
• v/c=0.5 avec un angle de 60°

Le cône interne représente le cône de visée après déviation.

Précédent     Suivant

Février 2009
Mise à jour : 12 Avril 2010